Notación científica
La notación científica (o notación índice estándar) es un modo conciso de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar facilmente números muy grandes o muy pequeños.
Los números se escriben como un producto:
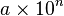
siendo:
 un número entero o decimal mayor o igual que 1 y menor que 10, que recibe el nombre de mantisa.
un número entero o decimal mayor o igual que 1 y menor que 10, que recibe el nombre de mantisa. un número entero, que recibe el nombre de exponente u orden de magnitud.
un número entero, que recibe el nombre de exponente u orden de magnitud.
La notación científica utiliza un sistema llamado coma flotante, o de punto flotante en países de habla inglesa y en algunos hispanohablantes.
La notación científica es un método práctico utilizado por los científicos para sintetizar una expresión matemática de base diez que resulta muy extensa, ya sea por lo pequeño que es o por ser un entero muy grande; en términos sencillos es una manera de representar un número muy grandes, usando unos pocos números, valiéndose de las potencias.
La notación científicas usa entonces las potencias, que consisten en multiplicar un número por si mismos varias veces. El número que hay que multiplicar lo indica la base, y las veces que hay que multiplicarlo lo señala el exponente. Por ejemplo 24 = 2 · 2 · 2 · 2 = 16. Siendo de esta manera el dos la base y el cuatro el exponente. En el caso de la notación científica, se de la misma manera las potencias, pero con base 10; esto sirve tanto para expresar números extremadamente grandes, pero también para números muy pequeños. Por ejemplo, la carga eléctrica de un electrón es de -1,6 x 10−19 .
Desde la Grecia Clásica es posible distinguir intentos de matemáticos por sintetizar la expresión de algún número. Como una anécdota curiosa, el famoso matemático y filósofo Arquímedes del siglo III AC fue el primero en utilizar la notación científica al tratar de contar cuántos granos de arena existían en el universo. El resultado que calculó fue de 1063 granos.
Este método, tal como comentábamos, es muy útil principalmente para aquellos textos que expresan números muy grandes. Por ejemplo, un texto de física que trata el tema de la luz, al referirse a su velocidad no la expresará en número, es decir, 300.000.000 m/s, sino que la simplificará a 3 · 108 m/s.
Cabe la posibilidad de que el exponente no sea un número positivo. En este caso, si el exponente nos señala un número negativo significa que el número es menor, por ejemplo 10-2, la cifra equivale a 0,1. Esto quiere decir que el exponente es negativo cuando se intentan expresar números menores a uno.
Como una regla práctica, podemos considerar para las potencias positivas de 10 que la potencia representa el "número de ceros" que le siguen al número uno. Por ejemplo 103 = 1 000, o sea es un 1 con tres ceros "añadidos". Ahora para las potencias negativas, como regla práctica podemos considerar que se representa el número de dígitos que corremos la coma hacia la izquierda del número uno, o si se prefiere, corresponde al número de ceros después de la coma menos un dígito. Por ejemplo 10-3 = 0,001 , o sea al 1 se le "corre" la coma tres dígitos a la izquierda, o también podemos pensarlo como (3-1)=2 ceros después de la coma tras el cero. Esta forma de verlo aunque no tiene valor técnico o científico, es de gran utilidad para trabajar con la notación científica cuando realizamos cálculos, o nos queremos imaginar la cifra de la que hablamos para poder cuantificarla en nuestra mente.
Los instrumentos matemáticos actuales utilizados por el mundo de la ciencia, las calculadoras científicas entre otros, todos consideran el método científico, incluyendo la tecla “E”, que al presionarla automáticamente considera al dígito como una potencia de base diez.
Existe otro tipo de notación llamada notación de ingería que tiene el mismo objetivo de la científica. La diferencia radica en que en la de ingeniería el exponente siempre es un múltiplo de tres y la base presenta límites definidos; debe estar ser entre el uno y el mil.
Escritura
- 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1 000
- 104 = 10 000
- 105 = 100 000
- 106 = 1 000 000
- 107 = 10 000 000
- 108 = 100 000 000
- 109 = 1 000 000 000
- 1010 = 10 000 000 000
- 1020 = 100 000 000 000 000 000 000
- 1030 = 1 000 000 000 000 000 000 000 000 000 000
10 elevado a una potencia entera negativa –n es igual a 1/10n o, equivalentemente 0, (n–1 ceros) 1:
- 10–1 = 1/10 = 0,1
- 10–3 = 1/1000 = 0,001
- 10–9 = 1/1 000 000 000 = 0,000 000 001
Por tanto, un número como: 156 234 000 000 000 000 000 000 000 000 puede ser escrito como 1,56234×1029,
y un número pequeño como 0,000 000 000 000 000 000 000 000 000 000 910 939 kg (masa de un electrón) puede ser escrito como 9.10939×10–31kg.
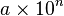
 un número entero o decimal mayor o igual que 1 y menor que 10, que recibe el nombre de mantisa.
un número entero o decimal mayor o igual que 1 y menor que 10, que recibe el nombre de mantisa. un número entero, que recibe el nombre de exponente u orden de magnitud.
un número entero, que recibe el nombre de exponente u orden de magnitud.- 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1 000
- 104 = 10 000
- 105 = 100 000
- 106 = 1 000 000
- 107 = 10 000 000
- 108 = 100 000 000
- 109 = 1 000 000 000
- 1010 = 10 000 000 000
- 1020 = 100 000 000 000 000 000 000
- 1030 = 1 000 000 000 000 000 000 000 000 000 000
10 elevado a una potencia entera negativa –n es igual a 1/10n o, equivalentemente 0, (n–1 ceros) 1:
- 10–1 = 1/10 = 0,1
- 10–3 = 1/1000 = 0,001
- 10–9 = 1/1 000 000 000 = 0,000 000 001
Por tanto, un número como: 156 234 000 000 000 000 000 000 000 000 puede ser escrito como 1,56234×1029,
y un número pequeño como 0,000 000 000 000 000 000 000 000 000 000 910 939 kg (masa de un electrón) puede ser escrito como 9.10939×10–31kg.
No hay comentarios:
Publicar un comentario